Aleph
A library for exploring persistent homology
Clique Community Persistence: A Topological Visual Analysis Approach for Complex Networks
This paper, which is available as a preprint on my personal website or as a full repository on OSF.io, deals with the analysis of complex networks. The basic idea is to decompose a network into its cliques and subsequently track their evolution using a modified variant of persistent homology.
In essence, this means that we developed a new variant of persistent
homology that deals with the connectivity of cliques—similar to
the CFinder algorithm, but different in that
we use the weights of a network in order to track at which threshold
level cliques merge with each other. Our method is thus capable of
detecting more changes than traditional clique enumeration methods. In
the paper, we depict a lot of interesting use cases, such as the
comparison of families of networks by means of their topological
distances.
This tutorial briefly demonstrates how to obtain clique community persistence diagrams, as described in the paper.
Obtaining community persistence diagrams
For this to work, you require the Les Misérables co-occurrence network as provided by Mark Newman. Aleph is capable of reading lots of different graph formats, including GML, the Graph Modelling Language or Graph Meta Language.
After building Aleph, we now use the tool
clique_persistence_diagram to obtain clique communities. These are the
parameters that we used for the paper (we shall discuss them
afterwards):
./clique_persistence_diagram --ignore-empty --invert-weights lesmis.gml 20
This should result in the following output:
* Reading 'lesmis.gml'...finished
* Inverting filtration weights...finished
* Expanding simplicial complex to k=20...finished
* Expanded simplicial complex has 2922 simplices
* Extracting 20-cliques graph...finished
* 20-cliques graph has 0 simplices
* Extracting 19-cliques graph...finished
* 19-cliques graph has 0 simplices
* Extracting 18-cliques graph...finished
* 18-cliques graph has 0 simplices
* Extracting 17-cliques graph...finished
* 17-cliques graph has 0 simplices
* Extracting 16-cliques graph...finished
* 16-cliques graph has 0 simplices
* Extracting 15-cliques graph...finished
* 15-cliques graph has 0 simplices
* Extracting 14-cliques graph...finished
* 14-cliques graph has 0 simplices
* Extracting 13-cliques graph...finished
* 13-cliques graph has 0 simplices
* Extracting 12-cliques graph...finished
* 12-cliques graph has 0 simplices
* Extracting 11-cliques graph...finished
* 11-cliques graph has 0 simplices
* Extracting 10-cliques graph...finished
* 10-cliques graph has 0 simplices
* Extracting 9-cliques graph...finished
* 9-cliques graph has 2 simplices
* Storing output in '/tmp/lesmis_k09.txt'...
* Extracting 8-cliques graph...finished
* 8-cliques graph has 114 simplices
* Storing output in '/tmp/lesmis_k08.txt'...
* Extracting 7-cliques graph...finished
* 7-cliques graph has 846 simplices
* Storing output in '/tmp/lesmis_k07.txt'...
* Extracting 6-cliques graph...finished
* 6-cliques graph has 2937 simplices
* Storing output in '/tmp/lesmis_k06.txt'...
* Extracting 5-cliques graph...finished
* 5-cliques graph has 6092 simplices
* Storing output in '/tmp/lesmis_k05.txt'...
* Extracting 4-cliques graph...finished
* 4-cliques graph has 8302 simplices
* Storing output in '/tmp/lesmis_k04.txt'...
* Extracting 3-cliques graph...finished
* 3-cliques graph has 7700 simplices
* Storing output in '/tmp/lesmis_k03.txt'...
* Extracting 2-cliques graph...finished
* 2-cliques graph has 5011 simplices
* Storing output in '/tmp/lesmis_k02.txt'...
* Extracting 1-cliques graph...finished
* 1-cliques graph has 3062 simplices
* Storing output in '/tmp/lesmis_k01.txt'...
* Storing accumulated persistence values in '/tmp/lesmis.txt'...
./clique-persistence-diagram –ignore-empty –invert-weights lesmis.gml 20
Let us quickly discuss the parameters before taking a look at the
diagrams. The first parameter --ignore-empty is required because we do
not know the size of the maximum clique yet. By default, the tool stops
once it encounters the first empty persistence diagram. Since we start
with potentially cliques with up to 21 members (more about that in
a minute), the tool should just ignore empty persistence diagrams rather
than stop.
The second parameter --invert-weights instructs the tool to invert all
input weights. Hence, large values become small values and vice
versa. In the spirit of persistent
homology, we want
small weights in the network to correspond to a high degree of
similarity. The co-occurrence network uses hight weights to denote
characters that often occur in the same chapter. Hence, we need to
invert the weights if we want to capture the merging behaviour
correctly.
The next parameter denotes the filename. Note that the tool is presently able to read GML files, NET (Pajek) files, and simple edge lists. This should cover many important network formats. If yours is missing, please open an issue or think about contributing it yourself. I would be more than happy to integrate your code!
The last parameter gives the maximum dimension of a simplex for
calculating clique communities. This parameter is essentially k-1,
with k denoting the degree of the clique. Hence, our 1-clique
community persistence diagram actually models the connectivity of
different edges in the data—in essence, this is a sort of
reduced variant of connected components.
Please see the paper for more details.
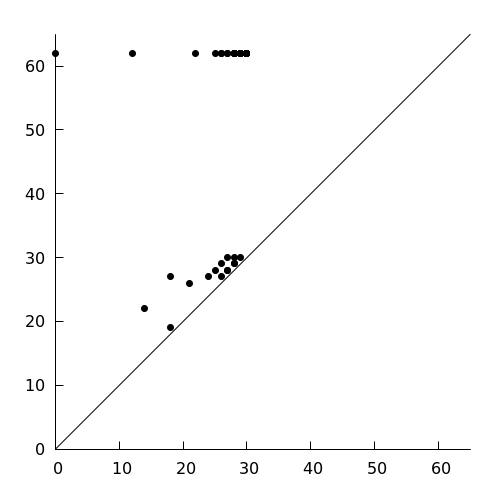
Now, as a final step, let us calculate a combined clique community
persistence diagram. From the output of the script, you can see that all
diagrams have been stored in /tmp. We can use the following
gnuplot script to visualize them together:
set xrange [0:65]
set yrange [0:65]
set key off
set border 3
set tics nomirror
set size square
plot "<cat /tmp/lesmi_k0?.txt" w p pt 7 lc rgb 'black', x lc rgb 'black'
The final result should look somewhat like this:
Stay tuned for more details and other applications!
More information
The following tools have been used to calculate and analyse networks in the paper: